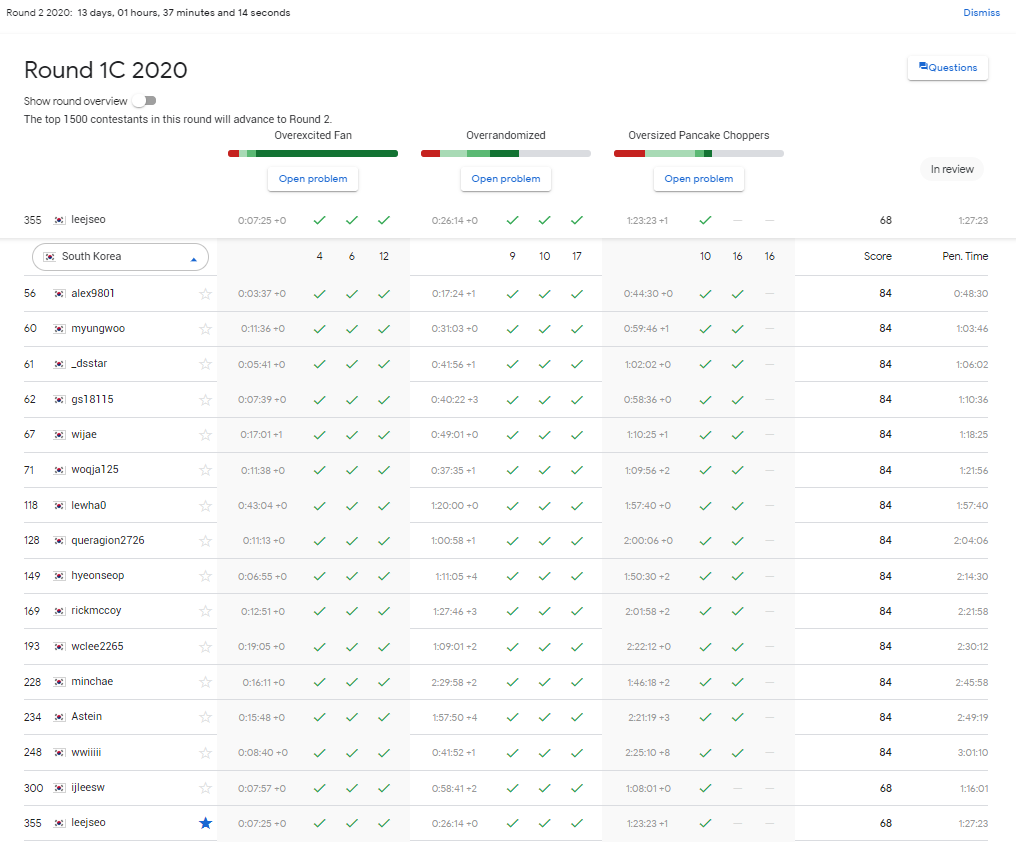
어제 참여한 Google Code Jam Round 1C에서 68점(패널티 1:27:23)으로 전체 355등을 하며 Round2에 진출하게 되었다. Round2는 약 2주 후에 개최된다. (문제/스코어보드 링크)
문제 풀이
A. Overexcited Fan
시각 $t$에 Peppurr의 위치를 $r(t) = (x(t), y(t))$라 하자. 이 때, 시각 $t$에 Peppurr를 만날 수 있을 필요충분조건은 $\mathrm{dist}(O, r(t)) = |x(t)| + |y(t)| \le t$가 됨을 확인할 수 있다. (단, $O$는 원점)
따라서, 각 $1 \le t \le \mathrm{len}(M)$에 대해 이 부분을 확인해주면 문제를 해결할 수 있다. 시간 복잡도는 총 $O(\mathrm{len}(M))$이다.
B. Overrandomized
먼저, $0$에 대응되는 문자 부터 찾자. $0$은 수의 맨 앞자리에 올 수 없으므로, 등장한 모든 문자들 가운데 맨 앞에 등장한적이 없는 문자가 $0$에 대응된다.
이제, 나머지 숫자들을 결정해주면 된다. 여기에서 핵심이 되는 관찰은 작은 수일 수록 등장할 확률이 높다는 것이다. 보다 엄밀하게는 $N = 10^U$라 할 때,
$$\begin{align*} \mathrm{Pr} (R_i = X) &= \sum_{k=X}^N \mathrm{Pr}(R_i = X | Q_i =k) \cdot \mathrm{Pr}(Q_i = k) \\ &= \sum_{k=X}^{N} \frac{1}{k} \cdot \frac{1}{N} \\ &= \frac{1}{N} \left( {1 \over X} + {1 \over X+1} + \cdots + {1 \over N} \right) \\ &\approx \frac{1}{N} ( \log N - \log X) \end{align*} $$
가 됨을 $\log n \approx \sum_{k=1}^n {1 \over k}$ 라는 사실로 부터 알 수 있다.
따라서, 맨 앞에 등장한 횟수가 큰 문자부터 순서대로 $1, 2, \dots, 9$에 대응된다.
import sys
inp = lambda : sys.stdin.readline().strip()
T = int(inp())
for t in range(T):
print ("Case #" + str(t+1) + ": ", end='')
U = int(inp())
S = set()
F = set()
cnt = dict()
for _ in range(10000):
q, r = inp().split()
q = int(q)
F.add(r[0])
if r[0] not in cnt: cnt[r[0]] = 1
else: cnt[r[0]] += 1
S |= set(list(r))
df = S - F
res = [df.pop()]
L = [ (cnt[key], key) for key in cnt ]
L.sort()
L.reverse()
for val, key in L: res.append(key)
print (''.join(res))C. Oversized Pancake Chopper
이 문제의 경우 Test Set 1만 해결해도 Round 2에 진출할 수 있는 상황이라 굳이 Test Set 2, 3을 풀지는 않았다. Test Set 1과 2에 대한 풀이만 적어두도록 하겠다.
Test Set 1
$D = 2$ 혹은 $D = 3$인 경우에 대해서만 해결하면 된다. $D= 2$인 경우, 크기가 같은 두 조각이 있으면 $0$, 아니면 $1$이 답이 된다.
$D = 3$인 경우는 조금 더 까다롭다.
- 크기가 같은 세 조각이 있으면 $0$,
- 크기가 같은 두 개의 조각만 있거나, 혹은 한 조각의 크기가 다른 조각의 두 배가 되는 쌍의 조각이 있으면 $1$,
- 아니면 $2$가 답이다.
Test Set 2
일단, 최악의 경우, 하나의 조각을 $D$등분 하게 되므로 답이 $D-1$이라는 점을 먼저 짚어두자.
어느 조각에서 잘려져 나온 모든 결과물을 serve 하게 된다면, 그 조각을 좋은 조각이라고 하자. 손님들에게 팬케이크를 나눠주는 과정에서 좋은 조각이 $X$개 있다면, 문제의 답은 $D-X$이다. 즉, 앞에서 말해둔 최악의 경우는 $X=1$인 경우라고 할 수 있다.
이 관찰에 의해 각 손님이 받게 되는 팬케이크의 크기는 $N/K$ (단, $K = 1, 2, \dots, D$)가 된다. 손님이 받는 팬케이크의 크기를 고정하면, 최소 칼질 횟수는 $O(N)$에 구할 수 있다. 손님이 받는 팬케이크의 크기는 총 $O(ND)$가지 경우가 있으므로, 총 시간 복잡도 $O(N^2D)$에 이 문제를 해결할 수 있다.
'Computer Science > Competition' 카테고리의 다른 글
| 2020 UCPC 예선 대비 개인 연습 (1) (3) | 2020.06.16 |
|---|---|
| 2019 ICPC 한국 리저널 인터넷예선 풀이 (1) | 2020.06.03 |
| Educational Codeforces Round 86 (1) | 2020.04.30 |
| 제1회 논산 코딩 페스티벌 풀이 (0) | 2020.04.12 |
| Google Hash Code 2020 참가 후기 (0) | 2020.02.21 |

