Note: 아직 미 완성인 글입니다.
20.06.03: A, B, C, D, F, H, I, J, L 풀이 수록
문제는 다음 사이트에서 일부 해결해볼 수 있다: 링크
A. All You Need is Dating
$i$번째 IC 학생이 원하는 데이트의 최소 횟수를 $minIC_i$, 최대 횟수를 $maxIC_i$로 표기하자. 비슷하게 $minPC_j$와 $maxPC_j$를 정의하자. 그러면, 이 문제는 아래와 같이 간선을 지나가는 유량의 최소 제한과 최대 제한이 있는 플로우 그래프로 모델링 가능하다.
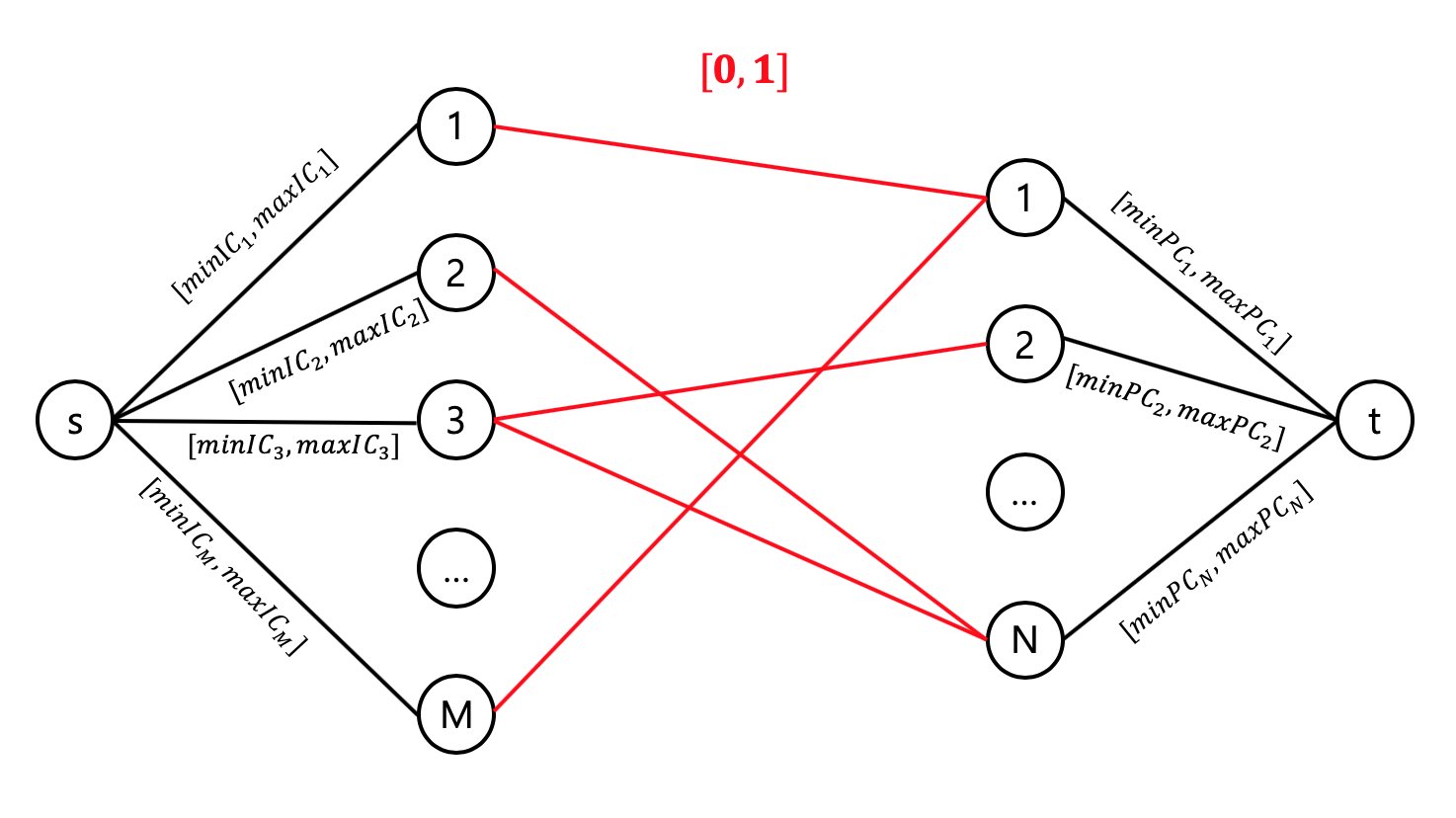
이는 전형적인 LR-flow 문제로, 해결법이 널리 알려져 있다. 일반적인 네트워크 플로우 알고리즘을 사용하여 해결하는 방법과 MCMF를 활용하는 방법이 있는데, 이 글에서는 생략한다.
B. Balanced String
$D[i][j = -1, 0, 1]$를 길이 $i$이고 $1$과 $0$의 개수 차이가 $j$인 균형잡힌 문자열의 수로 정의하면 동적 계획법을 통해 쉽게 해결할 수 있다. 혹은 이 점화식을 손으로 직접 해결하여 구현해도 된다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 16769023;
int N;
ll D[100005][3];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> N;
D[1][0] = 1, D[1][1] = 0, D[1][2] = 1;
for (int i=2; i<=N; i++){
D[i][0] = D[i-1][1];
D[i][1] = (D[i-1][0] + D[i-1][2])%mod;
D[i][2] = D[i-1][1];
}
cout << (D[N][0]+D[N][1]+D[N][2])%mod << endl;
}
C. Byte Coin
단순한 그리디한 방법을 통해 해결할 수 있다. $i$일에 다음과 같은 행동을 하면 된다:
- 모든 코인을 매도한다.
- $i+1$일의 가격이 $i$일보다 높으면, 코인을 최대한 많이 매수한다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int N;
ll W, A[20];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >>N >> W;
for (int i=0; i<N; i++) cin >> A[i];
for (int i=1; i<N; i++){
if (A[i] > A[i-1]){
ll c = W/A[i-1];
W -= A[i-1]*c;
W += A[i] * c;
}
}
cout << W << endl;
}
D. Canal
문제에 주어진 기하적인 상황이 다소 비직관적이므로, 다음과 같이 상황을 바꾸어 생각하자.
$n$개의 순서쌍 $(x_i, y_i) \in \mathbb{Z}^2$이 주어진다.
$\min_{a, b \in \mathbb{R}} \max_{1 \le i \le n} \min(|x_i - a|, |y_i - b|)$을 구하여라.
이 문제를 이분 탐색을 통해 접근한다면 다음과 같이 결정문제로 다시 쓸 수 있다.
$\max_{1 \le i \le n} \min(|x_i - a|, |y_i - b|) \le d$를 만족시키는 $a$, $b$가 존재하는가?
편의상 $(x_i, y_i)$가 $x$ 좌표 순으로 정렬되어 있다고 하자. $a$ 값을 골랐을 때 $|x_i - a| \le d$를 만족시키는 인덱스 $i$들은 연속적으로 위치한다. 따라서, 만약 인덱스들의 $y$ 좌표 값의 prefix/suffix min/max 값을 저장 해두었다면, 고정된 $a$에 대해 문제의 조건을 만족하는 $b$ 값의 존재성을 $O(1)$에 확인할 수 있다.
결론적으로, 결정문제를 해결하는 것은 투 포인터 기법을 통해 양 끝의 $x$ 좌표 값의 범위가 $2d$ 이하인 구간들을 살펴보면서 해결해주면 된다. 총 시간복잡도는 $O(n \log X + n \log n)$이 된다. 아래 구현을 보는 것이 풀이 이해에 더 용이할 것으로 생각된다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pi;
int N;
pi A[300005];
ll pmax[300005], pmin[300005];
ll smax[300005], smin[300005];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout << setprecision(1) << fixed;
cin >> N;
if (N == 1){
cout << 0.0 << endl;
return 0;
}
for (int i=1; i<=N; i++){
cin >> A[i].first >> A[i].second;
}
sort(A+1, A+N+1);
pmin[0] = smin[N+1] = (1E9)+1;
pmax[0] = smax[N+1] = -(1E9)-1;
for (int i=1; i<=N; i++){
pmin[i] = min(pmin[i-1], A[i].second);
pmax[i] = max(pmax[i-1], A[i].second);
}
for (int i=N; i; i--){
smin[i] = min(smin[i+1], A[i].second);
smax[i] = max(smax[i+1], A[i].second);
}
ll lo = 0, hi = ((ll) 2E9) + 1; // (lo, hi]
while (lo+1 < hi){
ll mid = (lo + hi)/2;
int st = 1, ed = 1;
bool able = false;
while (ed <= N){
while (st < ed && A[ed].first - A[st].first >= mid) st++;
ll m = (1E9)+1, M = -(1E9)-1;
if (st > 1){
m = min(m, pmin[st-1]);
M = max(M, pmax[st-1]);
}
if (ed < N){
m = min(m, smin[ed+1]);
M = max(M, smax[ed+1]);
}
if (M - m < mid){
able = true;
break;
}
ed++;
}
if (able) hi = mid;
else lo = mid;
}
cout << lo*0.5 << endl;
}E. Choreography
F. Dryer
가능한 $t$의 값이 총 $40 \le t \le 100$으로 61가지이다. 같은 $t$ 값을 가지는 옷들은 동시에 처리해줘도 됨은 명백하다.
$k$개의 dryer의 온도를 각각 어떤 값으로 고정시켰을 때 최소 시간안에 건조를 마치는데에 다음 전략이 유효하다.
$t$값이 작은 옷 부터 차례로 dryer에 다음과 같이 배정한다:
- $k$개 중 하나의 어느 dryer에 넣었을 때 해당 dryer의 작동시간에 영향을 주지 않는 경우, 그 dryer에 배정해주면 된다.
- 아니라면, 옷이 손상되지 않는 범위 내에서 가장 온도가 높은 dryer에 배정한다.
이 경우, 총 시간복잡도는 $O(61^{k+1})$이 된다.
G. Enumeration
H. Four Squares
$D[n]$을 합이 $n$과 같게 되는 제곱수들의 최소 개수로 정의하고 동적 계획법을 수행하면 된다. 총 $O(n \sqrt{n})$ 시간에 해결할 수 있다.
#include <bits/stdc++.h>
using namespace std;
int N;
int D[100001];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
fill(D, D+100001, 5);
cin >> N;
D[0] = 0, D[1] = 1;
for (int i=2; i<=N; i++){
for (int j=1; j*j<=i; j++){
D[i] = min(D[i], D[i-j*j]+1);
}
}
cout << D[N] << endl;
}
I. Registration
대회 전에 미리 DomJudge ID와 패스워드를 기록해둬야 해결할 수 있다. 대회 중에 이메일로 전송된 패스워드를 확인하는 것은 규정 위반이다.
J. Star Trek
$D[i]$를 $i$번 행성까지 가는데 걸리는 최소 시간으로 정의하여 동적 계획법을 활용하면 된다. $T[i]$를 행성 $i$에서의 준비 시간, $P[i]$를 행성 $i$에서 출발할 때의 pace, $A[i]$를 $1$번 행성으로 부터 거리라고 하면, 다음과 같은 점화식이 나온다:
$$D[i] = \min_{j < i} (P[j] \times A[i]) - P[j]A[j] +T[j] + D[j].$$
이는 직선 $P[j] x - (P[j]A[j] + T[j] + D[j])$의 $x = A[i]$ 에서의 최소값으로 생각할 수 있다. 따라서, Convex Hull Trick을 이용하여 $O(N \log N)$ 시간에 해결하면 된다. 나는 LineContainer.h 로 널리 알려진 자료구조를 사용했다. 자료구조 코드 출처: 링크
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
bool Q;
struct Line {
mutable ll k, m, p;
bool operator<(const Line& o) const {
return Q ? p < o.p : k < o.k;
}
};
struct LineContainer : multiset<Line> {
// (for doubles, use inf = 1/.0, div(a,b) = a/b)
const ll inf = LLONG_MAX;
ll div(ll a, ll b) { // floored division
return a / b - ((a ^ b) < 0 && a % b); }
bool isect(iterator x, iterator y) {
if (y == end()) { x->p = inf; return false; }
if (x->k == y->k) x->p = x->m > y->m ? inf : -inf;
else x->p = div(y->m - x->m, x->k - y->k);
return x->p >= y->p;
}
void add(ll k, ll m) {
auto z = insert({k, m, 0}), y = z++, x = y;
while (isect(y, z)) z = erase(z);
if (x != begin() && isect(--x, y)) isect(x, y = erase(y));
while ((y = x) != begin() && (--x)->p >= y->p)
isect(x, erase(y));
}
ll query(ll x) {
assert(!empty());
Q = 1; auto l = *lower_bound({0,0,x}); Q = 0;
return l.k * x + l.m;
}
} cht;
int N;
ll D[100005];
ll A[100005];
ll P[100005];
ll T[100005];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> N;
for (int i=1; i<N; i++){
cin >> A[i];
A[i] += A[i-1];
}
for (int i=0; i<N-1; i++){
cin >> T[i] >> P[i];
}
for (int i=1; i<N; i++){
cht.add(-P[i-1], A[i-1]*P[i-1]-T[i-1]-D[i-1]);
D[i] = -cht.query(A[i]);
}
cout << D[N-1] << endl;
}K. Steel Slicing
L. Two Machines
2015 KAIST 5th ACM-ICPC Mock Competition G번과 완전히 같은 문제이다.
$D[i][t]$를 $i$번째 작업까지 해결하면서 기계 $A$를 $t$시간 사용할 때 기계 $B$를 사용해야 하는 시간으로 정의하고, 동적 계획법을 사용하면 된다고 한다.
'Computer Science > Competition' 카테고리의 다른 글
| 2020 UCPC 예선 대비 개인 연습 (2) (0) | 2020.06.22 |
|---|---|
| 2020 UCPC 예선 대비 개인 연습 (1) (3) | 2020.06.16 |
| Google Code Jam Round 1C (0) | 2020.05.03 |
| Educational Codeforces Round 86 (1) | 2020.04.30 |
| 제1회 논산 코딩 페스티벌 풀이 (0) | 2020.04.12 |

