어떤 가중치 있는 (연결) 그래프 $G = (V, E, w)$가 있을 때, 트리 $T$가 $G$의 스패닝 트리 임은 $T$가 $G$의 부분 그래프이고, $V(T) = G(T)$(정점 집합이 같음)으로 정의된다. 최소 스패닝 트리(Minimum Spanning Tree, MST)는 스패닝 트리 가운데 모든 간선의 가중치의 합($\sum_{e \in E(T)} w(e)$)이 최소인 것을 의미한다. (최소 스패닝 트리는 여러개가 있을 수도 있다.)
예를 들어, 7개의 정점으로 이루어진 그래프 $G$가 있다고 하자.

이 때, 이 그래프의 MST는 다음과 같다:
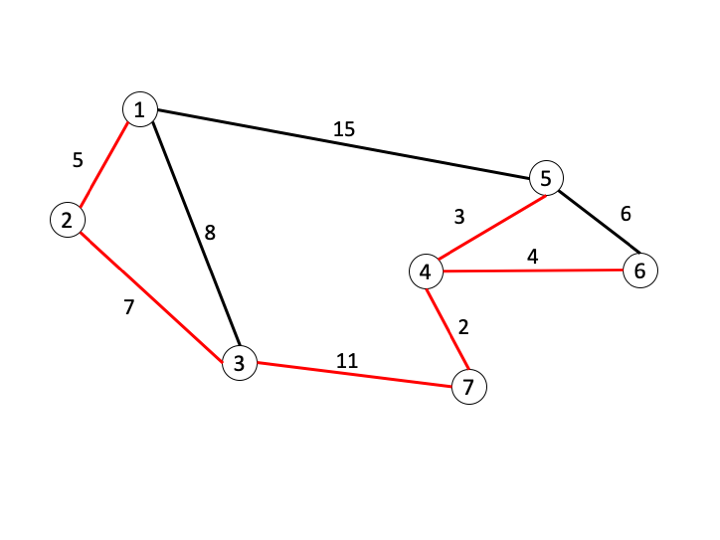
MST는 다음과 같은 알고리즘을 통해 $O(E \log E)$ 시간에 구할 수 있으며, 이는 Kruskal 알고리즘이라 불린다. 편의상 모든 간선의 가중치가 다르다고 하자.
Algorithm. Kruskal's MST Algorithm
input $G = (V, E, w)$
$T$ := $\emptyset$
sort $E = \{e_1, e_2 \dots, e_{|E|} \}$ so that $w(e_1) < w(e_2) < \dots < w(e_n)$
for $i$ := $1, 2, \dots, |E|$, do:
if $T + e_i$ contains no cycle:
$T$ := $T + e_i$
output $T$
이 알고리즘의 정당성을 설명하기 위해서는 MST의 성질을 알아야 하며, 이 글의 주된 주제이기도 하다.
Definition 1. (Cut)
정점 집합의 분할 $(S, T)$ 가운데 $S , T \neq \emptyset$인 것을 컷(cut)이라 한다. 정점의 한쪽 끝이 $S$, 다른 쪽 끝이 $T$에 놓이는 간선들의 집합 $D$를 cutset이라 부른다.
Property 1. Cycle $C$와 cutset $D$에 대해 $|C \cap D|$는 짝수이다.
증명의 경우 아래의 이미지를 보면 명확한데, 사이클을 따라 한 바퀴 돈다고 할 때, $S$에서 출발하면 $S$에서 끝나야 하므로, $S$와 $T$ 사이를 움직이는 횟수는 짝수번일 수 밖에 없다.
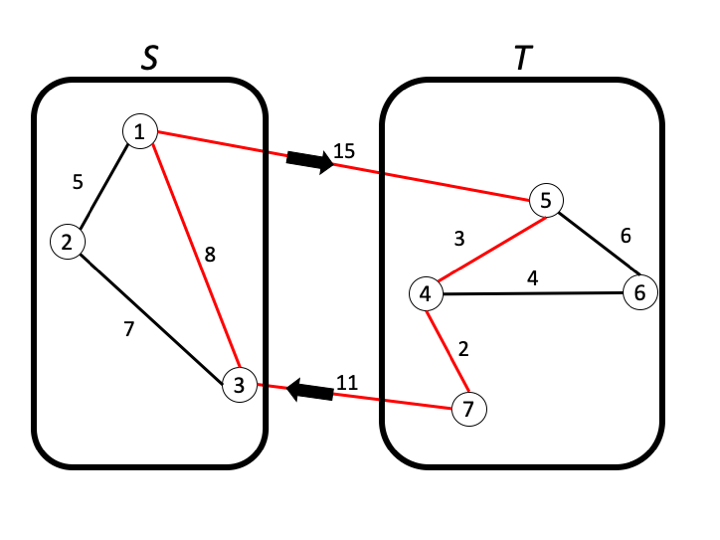
Property 2. (Cut Property)
임의의 cut set $D$에 대해 $D$에서 가중치가 가장 작은 간선 ($\mathrm{argmin}_{e \in D} w(e)$) 은 모든 MST에 반드시 포함된다.
Proof Sketch.
임의의 cut set $D$를 잡고, $D$에서 가중치가 가장 작은 간선 $e$를 택하자. $e$를 간선으로 포함하지 않는 MST $T'$이 존재한다고 가정하자. $T' + e$의 사이클 $C$를 잡자.
$C \cap D$는 짝수이고, $e \in C \cap D$이므로, $C \cap D$에 속하는 다른 간선 $f$를 잡아줄 수 있다. 그러면, $T = T' - f + e$ 또한 spanning tree가 되는데, $w(T') - w(T) = w(f) - w(e) > 0$이므로 $T'$이 MST임에 모순이다.

Property 3. (Cycle Property)
Cycle $C$에서 가중치가 가장 큰 간선은 아무 MST에도 포함되지 않는다.
Proof Sketch.
$f$를 포함하는 MST $T'$이 존재한다고 가정하자. $T' - f$의 두 컴포넌트에 의해 생기는 컷 $(S, V-S)$을 생각하자.
$(S, V-S)$에 대응되는 cutset을 $D$라 하자. 그러면 $|C \cap D|$는 짝수이고, $f \in C \cap D$이므로, 다른 간선 $e \in C \cap D$가 존재한다.
Spanning tree $T := T' - f + e$를 생각하면, $w(T') - w(T) = w(f) - w(e) > 0$이므로 $T'$이 MST임에 모순이다.
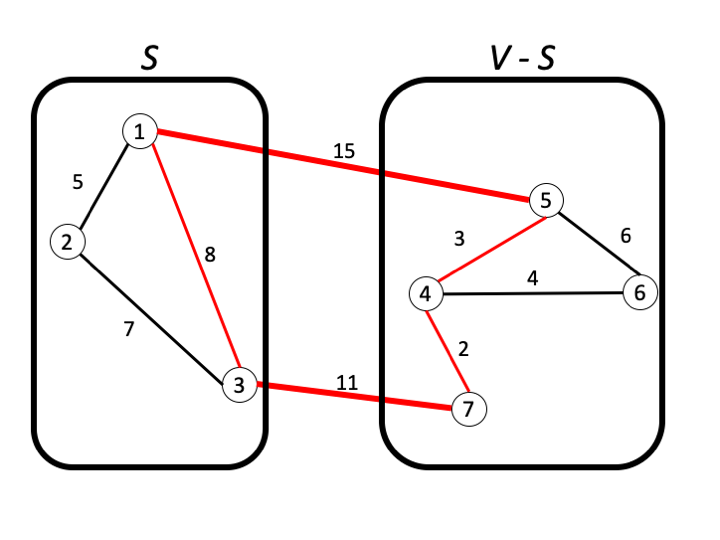
이제, Kruskal 알고리즘의 정당성에 대해 살펴보자.
Theorem. Kruskal's Algorithm은 올바르다.
Proof Sketch.
Kruskal's algorithm이 실행되면서 현재 "살펴보고" 있는 간선이 $e$라고 하자. 우리는 다음 두 가지 케이스의 정당성만 확인하면 충분하다:
- $T + e$가 cycle $C$를 포함하는 경우: cycle property에 의해 $C$에서 가장 가중치가 큰 간선인 $e$는 MST에 포함되지 않는다.
- 그렇지 않은 경우: $T+e$에 의해 합쳐지는 두 컴포넌트 중 하나를 $S$라고 하자. 컷 $(S, V-S)$에 대응되는 cutset $D$를 생각해보면, $e$는 $D$의 가장 가중치가 낮은 간선이다. 따라서, cut property에 의해 $e$는 MST에 포함된다.
위 정리에 의해 Kruskal's Algorithm이 정확함 또한 살펴보았다. 구현은 매우 간단하므로 따로 첨부하지 않으나, "$T + e$가 사이클을 포함한다"를 체크하는 스텝에서는 Disjoint Set 자료구조를 사용하면 됨은 짚어둔다.
P.S. 알고리즘 자체에 대한 보다 상세한 설명 및 MST를 구하는 다른 알고리즘인 Prim's algorithm을 담은 유익한 영상(링크)이 있으니 한 번 시청해봐도 좋을 것이다.
'Computer Science > Algorithms & Problem Solving' 카테고리의 다른 글
| Generalized Sorting with Predictions (3) | 2021.05.05 |
|---|---|
| Minimums on the Edges 풀이 (1) | 2020.10.19 |
| 최대 부분합과 쿼리 (0) | 2020.06.06 |
| Patience Sort (3) | 2020.05.24 |
| [UCPC 2018 예선 B] 카드 합체 놀이 (0) | 2020.03.11 |