이번에 UNIST 알고리즘 프로그래밍 경진대회에 3문제를 출제했다. 출제와 검수의 전 과정을 도울 수 있어서 기뻤고, 좋은 경험이었던 것 같다.
간단한 풀이는 아래와 같고, 문제 채점은 다음 링크에서 할 수 있다. https://acmicpc.net/category/detail/2353
A. 트리플 소트
- 출제: queued_q
문제에서 주어진 swap 연산으로는 기우성이 같은 인덱스 끼리만 바꿀 수 있음을 알 수 있다. 고로, 홀수 번째 인덱스와 짝수 번째 인덱스를 별개로 생각해볼 수 있다. 버블 소트를 생각해보면, 인접한 인덱스의 스왑 연산으로는 모든 배열을 정렬할 수 있음을 알 수 있다. 따라서, 홀수 번째 인덱스에는 홀수만, 짝수 번째 인덱스에는 짝수만 있는 것이 정렬 가능할 필요충분조건임을 알 수 있다.
여담으로, 문제의 제약조건이 상당히 친절하게 주어져 있다고 생각된다.
B. 타노스
- 출제: leejseo
증명은 어렵지만, 풀이는 단순하다. 0은 뒤에서부터, 1은 앞에서부터 지우면 된다. 증명의 경우 자잘한 논증 몇 개를 쌓으면 완성할 수 있다. 블로그에 적기에는 다소 더럽다고 생각되어, 굳이 적지 않는다.
C. 화학실험
- 출제: queued_q
먼저, 답이 없을 필요충분조건을 생각해보면, 하나의 색이 $\lfloor {N+1 \over 2} \rfloor$개 이상 있음임을 쉽게 확인할 수 있다. 이 경우를 걸러내고 나면, 개수가 많은 색부터 차례로 $1, 3, 5, ..., 2 \lfloor{N+1\over2} \rfloor -1, 2, 4, ..., 2 \lfloor {N \over 2} \rfloor$ 에 넣어주면 문제를 해결할 수 있다.
D. CPU 벤치마킹
- 출제: leejseo
문제가 장황한데, 결국 주어지는 배열의 모든 부분곱의 합을 구하는 문제다. 배열의 $i$번째 원소를 마지막 항으로 하는 부분곱의 합을 $D_i$라 하면, $D_i = (1 + D_{i-1}) m_i$ 라는 점화식을 얻게 된다. ($m_i$: 배열의 $i$번째 원소) 따라서, $O(N)$ 시간에 해결할 수 있다.
E. 출퇴근
- 출제: leejseo
간선의 가중치를 바꾸는 행위를 잘 모델링하는 방법을 생각해보자. 주목해야 할 점은, 마법을 한 번 쓰고 나면 되돌릴 수 없다는 점이다.
윤이가 $k$번째 마법을 쓴 이후의 가중치로 이루어진 그래프를 $G_k$라 하면, 아래 그림과 같이 $G_k$들을 층으로 쌓아주는 방법을 생각할 수 있다. 이러한 그래프의 맨 아래층의 시작 정점에서 맨 윗층의 끝 정점까지 최단거리를 구해주면 문제를 해결할 수 있다.
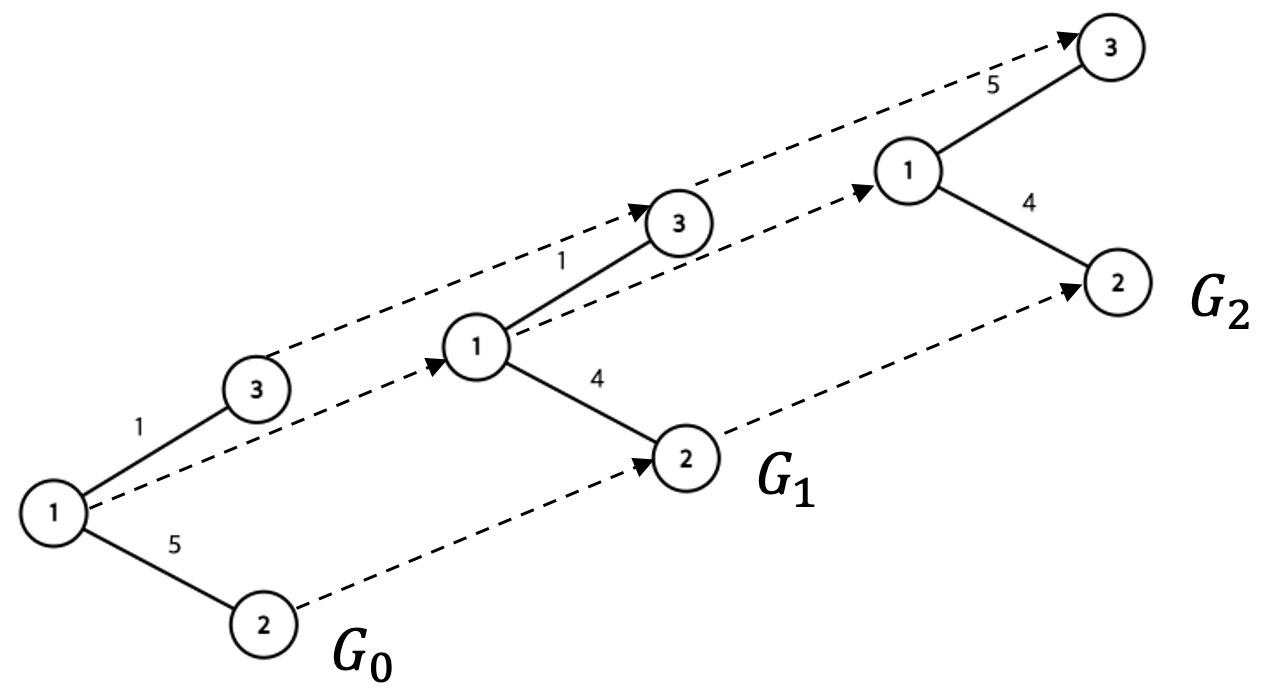
F. 대홍수
- 출제: queued_q
이 문제에서 해야하는 핵심적인 관찰은, 다음 두 가지가 있다.
- 하나의 정점에서 갈 수 있는 정점들은 구간의 형태로 나타난다.
- $i$번 정점이 갈 수 있는 구간을 $[l_i, r_i]$라 하면, $l_i$와 $r_i$ 모두 단조증가한다.
이 사실을 이용하면, $O(N)$시간에 각 정점이 갈 수 있는 구간을 구할 수 있다. 각 정점에 대해 $[l_i, r_i]$들을 모두 구하고 나면, 문제에서 요구하는 것은 구간 최대 쿼리(RMQ)로 바뀌게 되며, 이는 세그먼트 트리를 이용하면 쉽게 해결할 수 있다. 총 $O(N \log N)$ 시간에 해결할 수 있다.
다른 풀이로는 슬라이딩 윈도우를 이용해 전체 문제를 $O(N)$에 해결하는 풀이가 있는데, 내 풀이와 전반적인 방향은 유사하다.
G. 야바위
- 출제: queued_q
오프라인으로 문제를 해결하는 방법을 생각해보자. Set 자료구조에 구슬들을 넣어놓고, 시뮬레이션 하자. 이 경우 bottleneck이 되는 것은 두 컵의 내용물을 합치는 연산이다. 이 연산을 항상 작은 set에서 큰 set으로 합치도록 구현하면, 효율적으로 구현할 수 있다.
이 경우, 하나의 구슬이 크기 $x$인 set에 있다가 합치는 연산 후 크기 $y$인 set으로 이동했다고 하면, $y \ge 2x$가 항상 성립하기 때문에, 각 구슬은 최대 $O (\log K)$번 옮겨지게 된다. 따라서, hash 기반 set 자료구조를 이용하면 $O((N+M+K) \log K)$에, BBST 기반 set 자료구조를 이용하면 $O((N+M+K) \log^2 K)$ 정도에 문제를 해결할 수 있다.
'Computer Science > Competition' 카테고리의 다른 글
| SCPC 2020 짧은 후기 (1) | 2020.11.29 |
|---|---|
| ICPC 2020 Seoul Regional 후기 (4) | 2020.11.15 |
| ICPC 2020 Seoul Regional 예선 후기 (0) | 2020.10.15 |
| 2020 선린 정보 알고리즘경시대회 (3) | 2020.09.11 |
| UCPC 2020 참가 후기 (1) | 2020.08.01 |

