이 글에서는 분산 처리와 관련하여 최근에 제시된 두 계산 모델에 대해 간단히 알아본다. 또한, 그 계산 모델 상에서 돌아가는 잘 알려진 (그러면서도 이론적으로 중요한) 문제에 대한 알고리즘 및 계산 이론적 결과를 알아본다.
다만 이 주제에 대해 deep 하고 formal한 내용은 전혀 다루지 않는다. 전반적으로 두 계산 모델에 대한 이해를 조금 만드는 정도를 목표로 한다.
이 글에서 "높은 확률"은 최소한 1 - (polynomially small) 이상이라 이해하면 좋다.
Massively Parallel Computing Model (MPC)
먼저, Massively Parallel Computing Model(MPC)에 대해 알아보자. MPC는 다음으로 구성되는 계산 모델이다:
- 입력 데이터 크기 $N$
- 머신의 수 $M$
- 머신들은 서로 communicate 한다.
- 각 머신의 메모리 크기 $s$: 각 머신은 $s$개의 word를 들고 있을 수 있다.
여기에서 흥미로운 경우는 당연히 $M \cdot s = \Theta(N)$ 내지는 $M \cdot s = \Theta(N \text{polylog} N)$ 정도로 사용 가능한 전체 메모리 양이 입력의 크기와 엇비슷한 경우다. 이 계산 모델에서 입력과 출력에 대한 가정이 몇 가지 있다:
- 입력 데이터는 $M$개의 머신에 아무렇게나 쪼개진 채로 주어진다.
- 일부 머신은 "출력 머신"이 된다.
- 계산 과정이 종료된 이후, 출력 값은 출력 머신(들)에 들어 있을 것이다.
그림을 통해 이 가정들에 대한 이해를 높여보자. 아래 그림은 정수 배열 $A[]$가 $(i, a_i)$의 형태로 여러 머신에 걸쳐 주어지는 예시이다.

아래 그림은 앞 예시의 배열에 대한 prefix sum이 세 개의 출력 머신에 저장되어 있는 예시이다.

MPC 계산 모델에서 "계산"은 여러 라운드를 걸쳐서 진행된다. 각 라운드는 다음과 같은 2개의 phase로 구성된다:
- 각 머신은 자신의 메모리에 들어 있는 데이터를 이용해 적절한 계산을 한다.
- 각 머신이 다른 머신에게 message를 보내거나 받는다.
이 때, 각 머신은 매 라운드에 $s$ words만 주고 받을 수 있음에 유의하라. 결국, 지금까지 살펴본 MPC 계산 모델에 등장하는 주요 파라미터를 정리해보자면 다음과 같다:
- The number of machines, $M$ (mostly omitted)
- The number of communication rounds of an algorithm
- The size of local memory $s$
메모리의 크기와 관련해서는 주로 $s = O(N^\varepsilon)$ for $\varepsilon < 1$을 가정한다.
우리가 이 계산 모델상에서 주로 찾고자 하는 알고리즘은 "sublinear" 알고리즘이다. 어떤 알고리즘이 sublinear 함은 $s \ll N$ 임을 의미한다. (Formal 하게 적자면, $s = N^\varepsilon$ for some constant $\varepsilon < 1$.) 예를 들어, dense graph 상에서의 문제를 푸는 어느 MPC algorithm이 $s = n^{1 + \delta} (\delta < 1)$ 이라면, sublinear 하다고 말 할 수 있겠다.
Warming Up: Prefix Sum
이제 가장 간단한 알고리즘 문제 중 하나인 Prefix Sum 문제를 이 계산 모델 상에서 풀어보자. Prefix Sum 문제의 입력, 출력 형식을 정의하자면 다음과 같다:
- 입력: $n$ pairs of integers $(0, a_0) , (1, a_1), \cdots, (N-1, a_{N-1})$
- 출력: $(i, \sum_{j = 0}^k a_j)$ for $0 \le i < N$
이 문제에서 우리는 $M, s = \Theta(N^{0.5})$ 인 경우를 생각할 것이다. 실제 예시를 통해 Prefix Sum 문제에 대한 MPC 알고리즘을 알아보자.
Algorithm
먼저, 다음과 같이 입력이 주어져있다고 하자.

첫 round에서 먼저 각 머신은 자신이 들고 있는 $(i, A_i)$ 값을 $\lfloor \frac{Mi}{N} \rfloor$으로 보낸다.
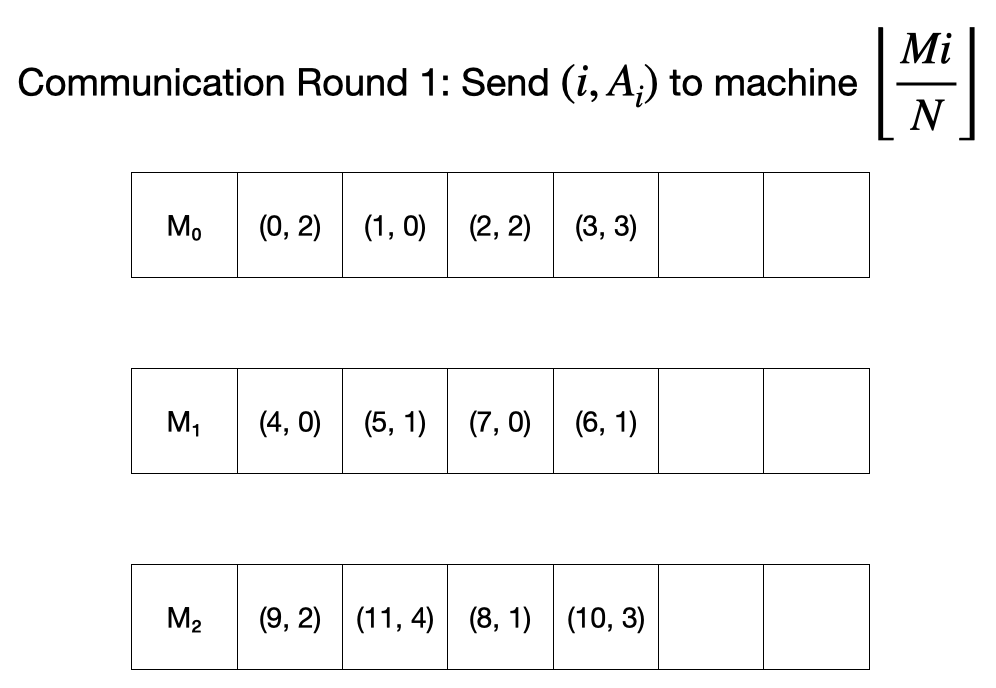
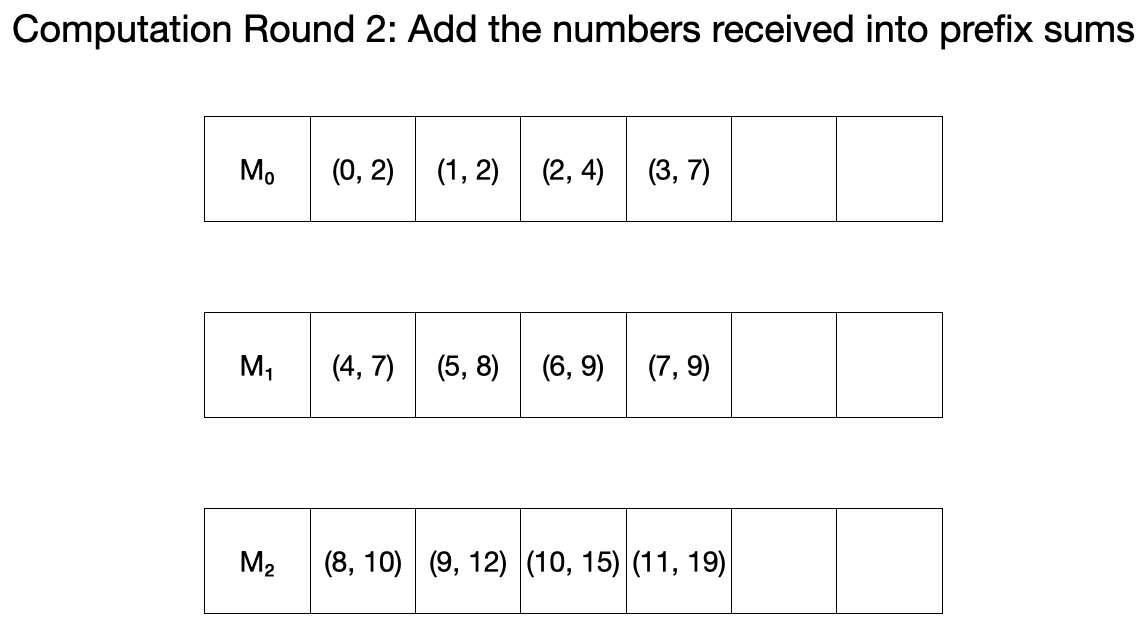
이후 각 머신은 자신이 들고 있는 튜플들을 sort 하고 이들의 prefix sum을 각각 계산한다.


두 번째 round에서 각 머신은 먼저 자신이 들고 있는 원소들의 총 합을 자신보다 인덱스가 큰 다른 머신에 보낸다.

이후, 각 머신은 자신이 받은 수들을 prefix sum들에 더해준다.
Overview
우리는 Prefix Sum을 MPC 세팅 하에 계산하는 과정을 살펴봤고, 이를 그림으로 요약하자면 다음과 같다.

이 알고리즘에서 $M = N^{0.5}$, $N = 2 \times N^{0.5}$ 정도로 잡아주면, 우리는 $O(N^{0.5})$ words of memory를 가지는 머신 $O(N^{0.5})$대를 사용한 것이 되고, $O(1)$ rounds of communication을 했고, 이 과정에서 오간 총 단어 수는 $O(N)$이 된다.
Maximal Matching
Maximal Matching 문제의 정의 부터 보자면, 다음과 같다. Maximum이 아니고 Maximal임에 유의하라.
- Instance: A graph $G = (V, E)$
- Question: Return a matching $M \subseteq E$ such that every edge in $E \setminus M$ having an endpoint in $M$
이 문제에 대한 MPC 알고리즘을 살펴볼 것이다.
기본적인 아이디어는 문제의 크기를 하나의 머신에서 해결할 수 있을 정도로 줄이면 쉽게 해결할 수 있음에 착안하며, 문제의 크기를 줄이기 위해 edge set의 subset에 대한 maximal matching을 single machine에서 잘 계산하고, match 된 edge들을 제거해나간다. 참고로, Dense한 그래프에 대해서만 효율적인 알고리즘이다.
Algorithm
우리가 살펴볼 알고리즘은 다음과 같다. (Note: $s = n^{1 + \varepsilon}$)

이 알고리즘의 running time(rounds)은 $\varepsilon$에 depend 함을 참고하라. 즉, 메모리를 얼마나 $n$(그래프의 크기가 아니고 정점의 수다.)에 가깝게 잡느냐에 따라 다르다.
Analysis
Round 하나를 고정하고, 해당 round의 시작 시점에 남아 있던 간선의 수를 $m$이라 하자. 간단한 계산을 통해 다음 두 Lemma를 증명할 수 있다.
Lemma. 높은 확률로 marked edge의 수는 하나의 머신에 들어간다.
Lemma. 높은 확률로 round가 끝난 후 남는 간선의 수는 $\frac{10m}{n^\varepsilon}$ 이하이다.
이 두 Lemma를 기반으로, 고정된 $\varepsilon$에 대해 전체 round의 수 $R$이 상수임을 보일 수 있다.
Theorem. 알고리즘은 $R = O({1}/{\varepsilon})$ round 만에 종료한다.
Proof. 처음에 최대 $n^2$ 개의 간선이 있다.
$R \le \log_{n^\varepsilon}n^2 = O(1 / \varepsilon)$ rounds를 지나고 나면 두 번째 Lemma에 의해 최대 $s = n^{1 + \varepsilon}$개의 간선이 남는다. $\square$
Connected Components
이번에는 connected components(ConnComp) 문제에 대한 알고리즘을 살펴보자.
- Instance: An undirected graph $G = (V, E)$
- Question:
- Which vertices are in the same connected component?
- A solution is a labeling $\ell$ of vertices s.t. $\ell(u) = \ell(v)$ if there's path from $u$ to $v$
우리가 살펴볼 알고리즘은 sparse한 graph를 다루기 위한 아이디어와 dense한 graph를 다루기 위한 아이디어를 조합하여 구성된다. 자세한 알고리즘 및 분석은 지면의 관계상 다루지 않고, 큰 그림에서 아이디어들을 살펴본다.
Graph Exponentiation: Handling Sparse Graph
Sparse graph를 잘 다루기 위해 graph exponentiation 이라는 연산을 사용하는데, 바로 각 정점을 이웃의 이웃과 연결해주는 것이다.
이 operation을 $O(\log D)$ ($D$: diameter)회 정도 반복하고 나면 각 연결 요소는 clique이 된다.
다만, 이 operation의 문제점이 있는데, 바로 개별 머신에서 요구되는 메모리의 양이 $\Omega(n^2)$이 될 수도 있다는 것이다.
Label Contraction: Handling Dense Graph
Label contraction이란 각 정점을 $p$의 확률로 독립적으로 mark 하고, 각 unmarked vertex을 이웃한 marked vertex의 label로 relabel하는 것이다.
Graph가 dense할 수록 $p$가 작아도 label이 잘 contract 된다.

Combining Together
기본적으로, 이 두 아이디어를 조합하여 다음의 과정(phase)을 반복하게 된다:
- Graph exponentiation을 수행하여 node들을 일종의 "supernode"로 collapse 한다.
- Label contraction을 수행한다.
여기에서 적절한 $p$를 잘 설정하면 각 phase가 $O(\log D)$ 개의 round를 사용하고, $O(\log_{m/n}n)$ 개의 phase를 수행하면 충분함을 확인할 수 있고, 이를 통해 $O(\log D \cdot \log_{m/n}n)$의 round complexity를 가지는 sublinear algorithm을 얻을 수 있다. 자세한 것은 reference의 자료들을 참고하면 좋다.
Hardness Conjectures & Results
지금까지 살펴본 결과들이 사실은 single machine에서 통상적인 크기의 입력에 대해서 푸는 것은 매우 쉬움에도 불구하고 (심지어 그리 좋지 않은 결과더라도) 알고리즘과 그 분석이 상당히 복잡했다.
이러한 MPC 세팅 하에서 풀기에 어렵다고 널리 받아들여지는 문제들에 대해 알아보자.
2-Cycle Problem.
- Instance: A graph that is either one cycle or the union of two cycles
- Question: Determine if the graph is one cycle or the union of two cycles
2-Cycle Conjecture. Any sublinear MPC algorithm for the 2-cycle problem requires $\Omega(\log n)$ rounds
심지어, 입력 그래프로 길이 $n$의 사이클 혹은 길이 $n/2$의 사이클 두 개가 주어질 때, 둘 중 어느 케이스에 속하는지 판별하는 것 조차 어렵다고 믿어진다.
이렇게 단순한 문제조차 어렵다 보니, 꽤 많은 문제들이 MPC 세팅 하에서 어렵다. 예를 들어 주어지는 그래프가 연결 그래프인지 확인하는 것 또한 $\Omega(\log n)$ rounds를 사용해야 한다. 왜냐하면, 이를 해결할 수 있으면 2-cycle Problem 또한 해결할 수 있기 때문이다. (reduction)
이와 관련하여 그래프 문제에 대해 Component-stable MPC algorithms 라는 개념이 있는데, 바로 각 정점에 대한 출력 값이 속하는 connected component에 depend하는 것을 의미한다. 이에 대해 다음이 알려져 있다.
Theorem. 2-cycle conjecture를 가정하면 sublinear component-stable MPC algorithm에 대해 다음이 성립한다:
- Maximal matching 혹은 그의 constant factor approximation에는 $\Omega(\log \log n)$ rounds를 필요로 한다.
- 임의의 상수 $c$에 대해 cycle을 $c$-coloring 하는 데에는 $\Omega(\log \log^*n)$ rounds를 필요로 한다.
- Vertex Cover에 대한 constant factor approximation에는 $\Omega(\log \log n)$ rounds를 필요로 한다.
- (더 많은 것을 가정하면) 그래프를 $(\Delta + 1)$-coloring 하는 데에는 $\Omega(\sqrt{\log \log n})$ rounds를 필요로 한다.
Adaptive Massively Parallel Computing Model (AMPC)
MPC 모델에 shared random access memory 개념을 추가한 Adaptive Massively Parallel Computing Model (AMPC)에 대해 알아보자.
이 계산 모델의 $i$ 번째 라운드에서 각 머신은 이전 라운드 직후 상태의 shared memory $D_{i-1}$을 읽고 새 shared memory $D_i$에 쓸 수 있다. 이 $D_{*}$ 들은 모든 머신에 걸쳐서 공통으로 제공되며, 한 라운드에서 각 머신은 최대 $S$회의 읽기와 $S$회의 쓰기를 shared memory에 할 수 있다. ($S$와 $s$는 다름에 유의하라.)
예를 들어, 함수 $g : X \to X$가 있고, ${(x, g(x)): x \in X} \subseteq D_{i-1}$ 이라면, 어떤 $y \in X$와 $k \le S$에 대해 $g^k(y)$를 계산하는 것이 AMPC 세팅 하에서는 가능하다.
당연하지만, AMPC는 MPC 만큼은 강력하다. 그렇다면, AMPC가 MPC보다 더 강력하다고 말 할 수 있을까? 그 근거가 2-cycle problem에 있다.
2-Cycle Problem: AMPC vs MPC
앞서 MPC에서 2-cycle problem의 subproblem인 길이 $n$의 사이클과 길이 $n/2$의 사이클 두 개를 구분하는 문제 또한 MPC 하에서는 $\Omega(\log n)$ rounds를 필요로 한다고 추측됨을 살펴봤다. (앞으로는 편의상 2-cycle problem이 방금 언급한 버전을 의미한다고 가정하자.) 이 섹션에서는 AMPC 세팅 하에 $O(1)$ round complexity를 가지는 2-cycle problem에 대한 알고리즘을 알아본다.
2-cycle problem에 대한 AMPC 알고리즘으로는 다음이 알려져 있다:

이 알고리즘과 관련해서는 다음의 lemma들을 간단한 계산을 통해 보일 수 있으며, 이를 통해 $s = O(n^\varepsilon)$ (sublinear)임과 $O(1/\varepsilon) = O(1)$ round complexity를 가짐을 보일 수 있다.
Lemma. $G$가 cycle(들)로 구성된 정점 $n$개의 graph라 하자. $SHRINK(G, \varepsilon, O(1/\varepsilon))$ 에서의 iteration 단계를 고정하자. Iteration의 시작 시 크기가 $\Omega(n^\varepsilon)$ 이상이었던 cycle은 높은 확률로 iteration 이후 크기가 $\Omega(n^{\varepsilon/2})$배 이상 줄어든다.
Lemma. SHRINK operation들 이후 각 cycle의 크기는 높은 확률로 $O(n^\varepsilon)$이 된다.
Lemma. 각 머신의 round 당 total communication은 높은 확률로 $O(n^\varepsilon)$회 일어난다.
AMPC vs MPC
AMPC 상에서의 SoTA algorithm과 MPC 상에서의 SoTA algorithm을 비교하자면 다음과 같다. 여러 문제에 대해 MPC보다 더 잘 함을 확인할 수 있다.

Hardness Results
AMPC에서의 hardness result로 다음이 알려져 있다. 참고로, 아래 정리에서 2-cycle problem은 원래 버전을 의미한다.
Theorem.
- 2-cycle 문제에 대한 임의의 결정론적 AMPC 알고리즘은 $\ge \frac{1}{2} \log_S(n/2)$ 회의 round를 사용한다. ($S = n^\varepsilon$ 이라면, $\Omega(1/\varepsilon)$)
- 2-cycle 문제에 대한 "좋은"(informal) randomized AMPC 알고리즘은 $\ge \frac{1}{2} \log_S(n/2)$ 회의 round를 사용한다. ($S = n^\varepsilon$ 이라면, $\Omega(1/\varepsilon)$)
Reference
- Computational Intractability: A Guide to Algorithmic Lower Bounds; https://hardness.mit.edu/
- S. Behnezhad et al. Massively Parallel Computation via Remote Memory Access. ACM Transactions on Parallel Computing, Vol. 8, No. 3
- Massively Parallel Algorithms http://people.csail.mit.edu/ghaffari/MPA19/Notes/MPA.pdf
'Computer Science' 카테고리의 다른 글
| Growing a Language: Go는 좋은 언어인가? (0) | 2025.12.07 |
|---|---|
| Unique Games Conjecture에 대한 노트 (2) | 2022.11.13 |
| The Short-Side Advantage in Random Matching Markets (0) | 2022.10.01 |
| Computational Complexity Classes (0) | 2022.09.29 |
| Redis는 어떻게 key를 expire 하는가? (2) | 2022.09.14 |