[퍼즐] 한 변의 길이가 1+ε인 정육각형

이번에 2025 조합론 워크샵에 다녀왔다. 많은 유익한 강연들이 있었고, 다양한 사람들과 이야기를 나누어 볼 기회가 있어서 좋았다. 워크샵에서 한 학교 후배가 알려준 퍼즐이 재밌어서 공유해본다.

 

한 변의 길이가 1+ε이고, 아랫변과 윗변이 x축에 평행하게 놓인 정육각형을 한 변의 길이가 1이며 세 변 중 하나가 x축에 평행한 단위 정삼각형으로 덮는 상황을 생각해보자. (아래 그림과 같이 두 종류의 정삼각형이 있을 것이고, 반드시 각 정삼각형의 한 변은 x축과 평행해야 한다.) 이 때 최소 몇 개의 정삼각형이 필요할까? (정삼각형 끼리 겹치는 것은 허용된다. 즉, packing이 아닌 covering 문제다.)

 

아래는 나의 간략한 풀이다. 풀이를 접어 두었으니, 충분히 고민해보고 열어보는 것을 추천한다. 어렵지 않다!

일단 여덟개의 정삼각형으로 덮을 수 있음은 쉽게 확인할 수 있다: (파워포인트로 대충 그려서 아다리가 잘 안맞는 것은 양해바람)

 

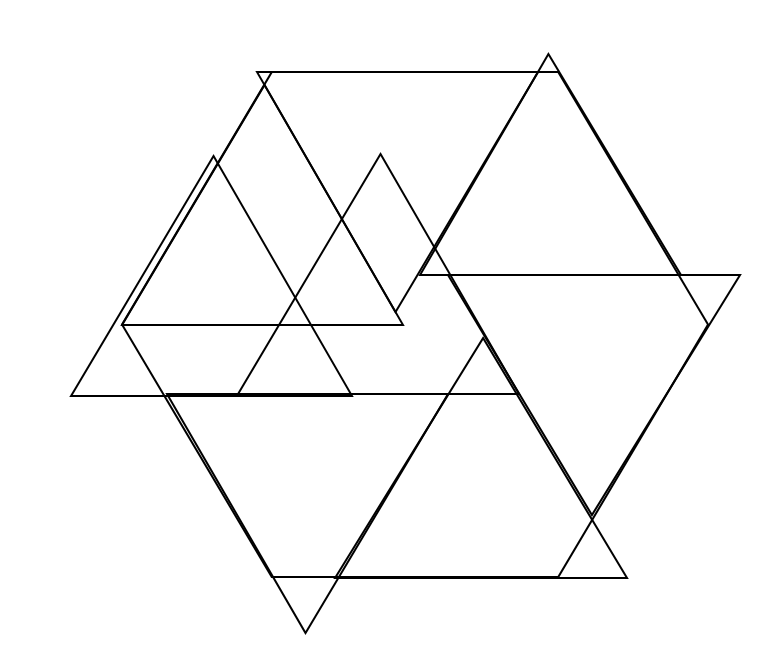
열심히 해 보면 일곱 개로 덮을수 없음을 추측할 수 있다. 이것을 증명하는 것은 약간 까다로운데, 다음과 같은 사실을 관찰할 수 있다.

 

먼저, 단위 정삼각형을 어떻게 배치하든 육각형의 "테두리"와 단위 정삼각형의 교집합은 유한개의 선분으로 나타낼 수 있다. 그리고 각 정삼각형과 육각형 테두리의 교집합의 "길이"는 최대 1이다. 따라서, 육각형의 "테두리"를 전부 덮기 위해서는 최소 7개 이상의 정삼각형이 필요하다.

 

그런데, 한 변이 x축에 평행한 단위 정삼각형은 육각형의 중심을 자신의 내부에 포함할 수 없다. 따라서, 육각형을 덮기 위해서는 최소 8개(테두리를 덮기 위한 7개 + 앞 7개로 커버되지 않는 중심을 덮기 위한 1개) 이상의 정삼각형이 필요하다.

 

참고로, 백진언 박사님의 논문과 관련 있는 퍼즐이라고 한다. https://arxiv.org/pdf/2306.09533

 

P.S. 워크샵 뒷풀이로 간 호프집에서 이 문제 고민하느라 친목을 충분히 즐기지 못해서 아쉬웠다. 그래도 재밌었다.